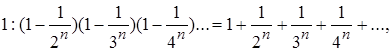
левая часть которой распространена на все простые, а правая на все натуральные числа; правая часть теперь известна как «дзета-функция Римана». Из этой формулы получается также, что ряд натуральных чисел содержит бесчисленное множество простых чисел, что, впрочем, было известно еще из доказательства Евклида. Но теорему о том, что всякая неограниченная арифметическая прогрессия, первый член и разность которой взаимно простые, также содержит бесчисленное множество простых чисел, Эйлер смог высказать лишь в качестве предположения («Аналитические сочинения», т. II, 1783). Это предположение высказал и Лежандр в Mem. Ac. Paris, 1785 (1788). Доказано оно было лишь Дирихле в 1837. Наконец, Эйлер занимался дружественными и совершенными числами, известными еще древним, причем для обозначения суммы делителей числа п он ввел символ , сохранившийся и в последующее время (Nov. Act. Erud., 1747 и «Сочинения различного содержания», т. II, 1750).

Стратегия свёртывания НЭПа
К 1926 году закончен восстановительный период. Страна вплотную подошла к новому периоду развития. Необходимость индустриализации, широкого обновления аппарата в промышленности, перевода предприятий на новый технический базис понимали все. Произвести на предприятиях страны новую технику было невозможно без обновления средств производства ...

Экономические взгляды Ермолая-Еразма
Среди церковной литературы, защищавшей интересы поместного дворянства, известный интерес представляют работы бывшего священника московской дворцовой церкви Ермолая-Еразма (середина XVI в:) Большая часть, его произведений посвящена богословию и нравственности, но в них ставились и социальные вопросы. Он был противником боярских центробеж ...

Упоминание в библии
Внимательно прочтем следующее место, записанное в форме Божьего обращения: Вот зверь, которого Я создал, как и тебя; он ест траву, как вол; вот его сила в чреслах его и крепость его в мускулах чрева его. Поворачивает хвостом своим, как кедром; жилы же на бедрах его переплетены. Ноги у него — как медные трубы, кости у него — как железны ...