Нужно еще добавить кое-что о разложении чисел на множители и о связанных с этим теоремах о простых числах. Уже Валлис в своем «Рассуждении о соединениях» (Discourse of Combinations, 1685) высказал теорему, гласившую, что всякое число можно разложить на простые множители единственным образом. Он выразил словесно важную формулу, согласно которой число делителей числа т= ., где р, q, r, . - простые числа, равно (l+1) (m+l)(n+1) ., и нашел, что сумма всех этих делителей равна

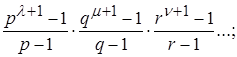
благодаря этому Валлис решил некоторые задачи, поставленные перед ним Ферма. Для нахождения самих делителей, именно простых делителей больших чисел, Эйлер предложил метод, основанный на представлении этих делителей в виде квадратичной формы mx2+ny2 [Nov. Comm. Ac. Petr., 1768 (1769) и Nouv. Mem. Ac. Bed., 1776 (1779)]. Исследования Лагранжа о подобных квадратичных формах также смогли быть применены к определению простых делителей. Ник. де-Бегелен разработал в Nouv. Mem. Ac. Bed., 1775 (1777) метод отыскания простых делителей вида 4х2+1. Эйлер в письме к Бегелену обратил его внимание на то, что эти делители можно получить из более общей формы nх2 + у2, и указал правило подходящего выбора числа п, давшее ему целый ряд больших простых чисел [Nouv. Mem. Ac. Berl., 1776 (1779)]. Наконец, десять лет спустя Эйлер указал общий признак, позволяющий решать, является данное число простым или составным [Nov. Act. Ac. Petr. 1797/98 (1805)].

Вместе с тем математики того времени тщетно искали общее, аналитическое выражение для представления простых чисел. Лежандр, которому удалось доказать, что это выражение не может быть рациональным, потерял всякую надежду на то, что его когда-либо удастся найти. Вероятно, такое аналитическое выражение не существует вообще. Столь же мало вероятно существование функции p(х), составленной конечным образом и точно представляющей число простых чисел, не превосходящих числа х. Теорему о том, что эта функция p(х) при возрастании х асимптотически приближается (строго доказанную лишь Ж Адама-ром и. Валле-Пуссеном в 1896), предвидел еще Лежандр, не имея, впрочем, никакого представления о ее доказательстве. Он именно нашел (в «Опыте», 1798 и, точнее, во втором издании 1808) эмпирическую формулу

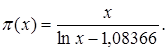
К разложению чисел на множители примыкает их разбиение на слагаемые, которые можно отнести к области аналитической теории чисел, т. е. к теоретико-числовым исследованиям, опирающимся на рассмотрения аналитического характера. Эйлер, посвятивший исследованиям этого рода 15-ю и 16-ю главы первого тома «Введения» (1748), и здесь опять указал путь вперед. Он исходил из разложения произведения

(1+xa z)(1+xb z)(1+xg z)

где a, b, g — положительные целые числа, в ряд

1+Pz+Qz2+Rz3+…

Отсюда немедленно следовало, что

Р = xa +xb +xg +…, Q = xa+b + xa+g+ …

и т. д., и было видно, что если показатель одной и той же степени может представлять сумму двух или нескольких членов ряда a, b, g различными способами, то такая степень имеет коэффициент, заключающий в себе столько единиц, сколько существует таких способов. Поэтому, если требуется узнать, сколькими способами можно представить число п в виде суммы т неравных членов рядаa, b, g, ., то это укажет коэффициент имеющегося в разложении члена хnzm. Аналогичным образом Эйлер рассмотрел дробь

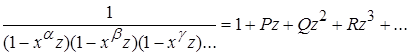
и вывел теорему, что коэффициент члена хпzm указывает, сколькими различными способами можно получить целое число я в виде суммы т равных или неравных чисел рядаa, b, g . Из этих двух главных теорем при тех или иных частных значениях z был получен ряд отдельных теорем об аддитивном разбиении чисел. Эйлер построил также таблицу, продолженную затем в Nov. Comm. Ac. Petr. [1750/51 (1753), см. также 1769 (1770)], в которой можно было прочесть, сколькими способами можно представить число п в виде сумм чисел 1, 2, 3, .,т. В указанных томах Nov. Comm. Ac. Petr. [см. также 1754/55 (1760)] он вывел отсюда так называемую пентагональную теорему, гласящую, что число разбиений числа п на четное число различных слагаемых равно числу разбиений на нечетное число слагаемых, кроме случая п , когда для т четного (нечетного) оно на единицу больше (соответственно, меньше). Тот же метод дал Эйлеру важную формулу

Особенности революции в Италии. Провозглашение Римской республики.
К середине XIX в. значительная часть Италии (Ломбардия, Ве­нецианская область) находилась под австрийским владычеством. В Парме, Модене и Тоскане правили родственники австрийских Габсбургов. В Римской области сохранялась светская власть папы, который также был противником национального объединения страны и прогрессивных преобразований. ...

Происхождение и ранняя история восточного славянства.
IV-VIIвв - великое переселение народов VIIIв - возникновение у восточных славян первой формы государственности (племенного княжения) Славяне относятся к индоевропейской семье народов (историки считают, что они обособились в середине II тысячелетия до н.э., а праславянский язык начал складываться в середине I тысячелетия до н.э.). Их п ...

Земельные реформы
Однако задачи, выдвинутые в Стоглаве, не были решены, что вылилось в открытое недовольство Ивана Грозного. Это недовольство выразилось в приговоре 11 мая 1551 г., когда покупка духовными землевладельцами вотчинных земель без “доклада” Ивану Грозному запрещалось под угрозой конфискации объекта продажи. О действенности приговора 1551 года ...