Другим приближенным методом, который покоился на совсем иной основе, чем способ Ньютона, и не нуждался в определении границ корней, был метод рекуррентных рядов, сообщенный Даниилом Бернулли в Comm. Ac. Petr., 1728 (1732). Возникновение этого метода было, впрочем, связано с замечаниями Ньютона о применении к решению уравнений сумм степеней корней. Способ Бернулли заключался в следующем. Пусть требуется решить уравнение

и пусть выбраны п произвольных чисел Р1, Р2, Р3, ., Рп. Если теперь определить Рп+1, Рп+2, . рекуррентным законом

(т=1, 2, 3, .), то отношение с возрастанием т приближается к наибольшему по абсолютной величине корню уравнения. Даниил Бернулли высказал эту теорему без доказательства. [12] Эйлер в 17-й главе «Введения» (1748) тщательно разобрал этот метод и привел отсутствовавший вывод.

Так как всякий рекуррентный ряд получается из развертывания рациональной дроби, то пусть эта дробь будет равна

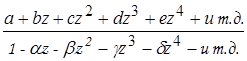
откуда получается рекуррентный ряд

А+Вz+Cz2+Dz3+Ez4+Fz5+ и т.д.

его коэффициенты А, В, С, D, и т.д. определятся так:

A=a, B=aA+b, C=aB+bA+c,

D=aC+bB+gA+d, E=aD+bC+gB+dA+e и т.д.

Общий же член, т.е. коэффициент степени zn, найдется из разложения данной дроби на простые дроби, знаменатели коих являются множителями знаменателя

1-az-bz2-gz3- и т.д.

Вид общего члена зависит, главным образом, от свойств простых множителей знаменателя, будут ли они действительными или мнимыми, а так же от того, будут ли они отличны друг от друга или два и более будут одинаковыми. Для последовательного рассмотрения этих различных случаев положим вначале, что все простые множители знаменателя действительны и не равны между собой. Пусть все простые множители знаменателя будут

(1-pz)(1-qz)(1-rz)(1-sz) и т.д.

и тогда данная дробь разложится на простые дроби.

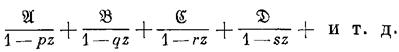
Когда они найдены, то общий член рекуррентного ряда будет равен

примем его равным Pzn; значит, P будет коэффициентом степени zn; у следующих же членов пусть коэффициенты будут Q, R, и т.д., так что рекуррентный ряд будет

А+Bz+Cz2+Dz3+…+Pzn+Qzn+1+Rzn+2+ и т.д.

Теперь положим, что п представляет чрезвычайно большое число, т.е. что рекуррентный ряд продолжен весьма далеко; так как степени неравных чисел тем более отличаются друг от друга, чем они больше, тем между степенями и т.д. будет такое различие, что степень, соответствующая наибольшему из чисел р, q, r и т.д. между собой не равны, то пусть p будет наибольшим среди них. Тогда, если п будет числом бесконечно большим, будем иметь

если же п будет числом не бесконечно, а лишь очень большим, то только приближенно будет Подобным образом будет и, следовательно.

Мир в новое время. Тридцатилетняя война: основные этапы конфликта и его итоги
Тридцатилетняя война 1618-1648,первая общеевропейская война между двумя большими группировками держав: стремившимся к господству над всем "христианским миром" габсбургским блоком (испанские и австрийские Габсбурги), поддержанным папством, католическими князьями Германии и Польско-Литовским государством (Речь Посполита), и прот ...

Приоритеты внешней политики Украины на рубеже ХХ-ХХI вв.
1. Конституция Украины о внешней политике государства. Почти 10 лет Украина является полноправным субъектом международных отношений. Конституцией Украины определен общий подход к внешней политике государства (Статья 18). Предусмотрено, что внешнеполитическая деятельность Украины направлена на обеспечение ее национальных интересов и бе ...

Князь и дружина.
Основным источником дохода князя помимо дани была военная добыча. Но уже в конце Xв появились княжеские села, хозяйство которых носило промысловый и коневодческий характер. Добываемая пушнина продавалась наряду с экспортной частью дани на рынках Константинополя. С умножением числа дружинников дани стало не хватать. Князья стали посылат ...