Отсюда ясно, что если рекуррентный ряд продолжить достаточно далеко, то коэффициент любого члена при делении на предыдущий дает приближенное значение наибольшей буквы р.

Итак, если у данной дроби

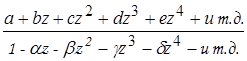
в знаменателе все сомножители простые, действительные и не равные между собой, то из получающегося отсюда рекуррентного ряда можно будет узнать один простой множитель, именно, 1-pz, в котором буква р имеет самое большое значение. При этом коэффициенты числителя не играют роли, и, каковы бы ни были, для наибольше буквы р найдется одно и то же верное значение. Верное же значение р обнаружится лишь тогда, когда ряд будет продолжен до бесконечности; когда получены уже многие его члены, то значение p найдется тем ближе, чем больше число членов и чем более буква р превосходит остальные q, r, s и т.д.; при этом безразлично, будет ли эта буква р сопровождаться знаком плюс или минус, так как степени ее возрастают одинаково.

Теперь в достаточной степени выясняется, каким образом это исследование может быть применено к нахождению корней, какого либо алгебраического уравнения. Зная множители знаменателя

1-az-bz2-gz3-dz4- и т.д.,

легко указать корни уравнения

1-az-bz2-gz3-dz4- и т.д. =0,

так, что если множитель будет 1-pz, то один корень этого уравнения будет z=. Так как из рекуррентного ряда найдется наибольшее число р, то тем самым получится наибольший корень уравнения

1-az-bz2-gz3- и т.д. =0,

Или если положить z=, чтобы получилось уравнение

xm-axm-1-bxm-2-gxm-3- и т.д. =0,

то посредством того же метода получится наибольший корень этого уравнения х=р.

Итак, пусть дано уравнение

xm-axm-1-bxm-2-gxm-3- и т.д. =0,

у которого все корни действительны и не равны между собой; наибольший из этих корней найдется следующим образом. Составим из коэффициентов этого уравнения дробь

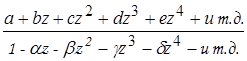
и отсюда образуем рекуррентный ряд, беря числитель произвольно или, что то же, принимая начальные члены произвольными; пусть этот ряд есть

А+Bz+Cz2+Dz3+…+Pzn+Qzn+1+ и т.д.

тогда дробь даст значение наибольшего корня х данного уравнения тем ближе, чем больше число п. [6]

п.2.2.2. Еще два оригинальных метода.

Кроме метода Бернулли, который сохранился до нашего времени в форме, сообщенной ему Лагранжем, XVIII столетие принесло еще два оригинальных метода И. Г. Ламберта. Оба они были изложены в статье «Различные замечания о чистой математике» (Observationes variae in mathesin puram в Acta Helvetica за 1758). Если в уравнении

сделать подстановку x = k+y и пренебречь всеми степенями у, кроме первой, то получится, что

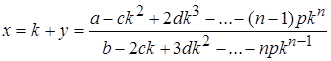
Когда k представляет собой какое-либо число, эта формула, согласно Ламберту, дает приближенное значение для корня, ближайшего к k. Второй метод заключался в применении ряда, получившего название ламбертова, к трехчленным уравнениям вида

Стратегия свёртывания НЭПа
К 1926 году закончен восстановительный период. Страна вплотную подошла к новому периоду развития. Необходимость индустриализации, широкого обновления аппарата в промышленности, перевода предприятий на новый технический базис понимали все. Произвести на предприятиях страны новую технику было невозможно без обновления средств производства ...

Рекомендации по определению этических и эстетических норм письменной коммуникации.
Учет некоторых рекомендаций, которые приводятся далее, может помочь специалисту по связям с общественностью при определении того, что этично в его поведении, а что нет. ...

Держава Ахеменидов.
Покорив за короткий срок ослабевшую Грецию, Филипп II решил объединить усилия своей страны с усилиями побеждённой им Греции и начать поход против Персидского государства, считавшегося в то время колоссом на глиняных ногах. Пёстрое в этническом, экономическом и социальном отношениях, оно с каждым днём слабело от внутренних восстаний, кот ...