В рассматриваемое время координатный метод употребляли преимущественно в дифференциально-геометрических исследованиях, или же, если подчеркивали значение метода Декарта, применяли его к высшим алгебраическим кривым. Последним занялся, в частности, де-Гюа-де-Мальв в небольшой книге «Применения анализа Декарта», которая была богаче новыми идеями, чем аналитическими выводами. Эти исследования более высокого порядка могли быть с таким же успехом приложены к коническим сечениям, которые иногда и привлекались в качестве примеров. Так, например, де-Гюа впервые дал для конического сечения

nyy+rxy+mxx+ay+bx+cc=0

(т, п, r обозначают числа, но а, b, с — отрезки) уравнение, определяющее координаты центра, в виде

Cледует упомянуть, что для де-Гюа было вполне привычным представление о кривой, распадающейся на несколько других, т. е. кривой, уравнение которой в левой части разлагается на ряд множителей. Он даже называл уравнение у3= х3 уравнением трех прямых, две из которых мнимые.

Сочинение Г. Крамера «Введение в анализ алгебраических кривых», опиравшееся во многих отношениях на работу де-Гюа и изданное десятью годами позднее, также ограничивалось высшими алгебраическими кривыми. Тем временем уже появился второй том «Введения в анализ» (1748) Эйлера, поднявший на существенно более высокую ступень и аналитическую теорию конических сечений. Эйлер целиком еще держался декартова понятия о координатах, между тем как Крамер, на сочинение которого книга Эйлера повлиять уже не могла, впервые равноправно определил две координаты и последовательно ввел ось ординат. Правда, в преобразованиях координат у Крамера ось ординат все еще играла несколько беспомощную роль. Со времен Витта преобразования координат употреблялись всеми математиками и нередко принимали даже довольно сложные формы, ибо тогда часто переходили от одной косоугольной системы к другой, с новым началом и отличным координатным углом, не пользуясь при этом тригонометрическими функциями. Впервые последними воспользовался для этой цели Эйлер во «Введении в анализ». Он еще часто обозначал синус или косинус угла посредством какой-либо специальной буквы. Но у него имелись уже и такие формулы преобразования прямоугольной системы:

t = x cos • q - у sin • q, u = x sin • q + y cos • q.

Во второй главе II тома «Введения в анализ», посвященной преобразованию координат, Эйлер коротко останавливается на вопросе о прямой. Сначала он приводит ее уравнение в виде a u+b t+b = 0, но затем, желая определить положение прямой, записывает его в виде a x+b y - a= 0. Он не разбирает различные возможные комбинации знаков a и b и упоминает лишь случаи a = 0, b = 0 и a = а = 0, не касаясь, однако, случая b=a=0. Все эти возможности были впервые разобраны, по крайней мере, в форме беглых замечаний, в книге Риккати-Саладини.

В пятой главе II тома «Введения в анализ» речь идет об общих свойствах всех конических сечений, т. е. свойствах, которые можно вывести из общего уравнения второй степени. Хотя вначале Эйлер определенно заявляет, что из одного принципа вывести все свойства конических сечений нельзя и что одни получаются из способа образования этих линий на конусе, а другие из приемов их описания, но здесь он желает опираться только на уравнение. Последнее он записывает в виде

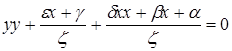
причем координатный угол в зависимости от обстоятельств берется то прямым, то отличным от прямого. Действуя вполне в духе Ньютона и Стерлинга, Эйлер в первую очередь выводит из этого уравнения на основании теоремы о сумме и произведении корней обычные свойства диаметров, секущих и касательных. К числу извлекаемых им следствий принадлежит также теорема, что коническое сечение можно рассматривать как геометрическое место к четырем прямым. Далее он определяет уравнение диаметра, делящего пополам хорды, параллельные ординатам, вначале в прямоугольной системе, а затем для того же конического сечения в системе с прежними осью абсцисс и началом, но с косоугольно расположенными ординатами. Точка пересечения обоих диаметров дает центр конического сечения, координаты которого не зависят от угла, образуемого направлением ординат с осью абсцисс. Затем Эйлер устанавливает отнесенные к «сопряженным диаметрам» уравнения

Интимная жизнь
Интимная жизнь османов была подчинена строгим религиозным правилам. Семья неприкосновенна, блюдется девственность. Зачатие, впрочем, остается священным долгом. Во многих строфах Корана говорится о том, что половые отношения — лишь естественная функция, служащая продолжению человеческого рода, и только мужчина может заявлять о своем секс ...

Александр Македонский
Александр Великий (Македонский) (356–323 до н.э.), царь Македонии, основатель мировой эллинистической державы; самый прославленный полководец античности. Родился в конце июля 356 до н.э. в Пелле, столице Македонии. Сын македонского царя Филиппа II (359–336 до н.э.) и Олимпиады, дочери молосского царя Неоптолема. Получил аристократическо ...

Подготовка сторон к войне.
И Россия и Франция готовились к войне. Со всей Европы сгонялись в армию Наполеона солдаты, свозились боеприпасы, продовольствие, фураж. К июню 1812 года армия, которую Наполеон называл «великой», насчитывала около 600 тысяч человек и имела 1200 артиллерийских орудия. Во главе их стояли прославленные маршалы и генералы. В России тоже ...