Во второй половине XVIII столетия прочное основание получила также дифференциальная геометрия общих поверхностей. Уравнение касательной плоскости к поверхности дали одновременно Тенсо и Монж в статьях (Mem. div. sav., IX, 1780). Обозначая координаты точки поверхности х, у, z, а координаты произвольной точки касательной плоскости π, φ, ω, Тенсо записал ее уравнение в виде

Заключенные в скобки дифференциальные частные нужно здесь рассматривать как частные производные. Кроме того, Тенсо рассмотрел задачу об определении линии прикосновения к поверхности касательного конуса, проведенного к ней из точки (а, b, с), как это сделал и Монж. Затем он разобрал такую же задачу для параллельных касательных и вопрос об установлении уравнений соответствующих конуса и цилиндра. Впрочем, для всех этих задач он ограничивался лишь указаниями. Готовые формулы или примеры отсутствовали. У Монжа уравнение касательной плоскости получило уже вполне современный вид:

z=p’ ( x - x’) + q’ (y – y’ ) + K’.

Эйлер в этой области также открыл ряд фундаментальных теорем. В одной большой работе о кривизне поверхностей [Mem. Ac. Berlin, 1760 (1767)] он прежде всего приступил к задаче об определении радиуса кривизны сечения данной поверхности, лежащего в плоскости z = α у—β x+γ причем получил, разумеется, весьма сложное выражение. Затем он провел секущую плоскость через нормаль к поверхности и вычислил новое выражение для радиуса кривизны сечения, нисколько не более простое, чем предыдущее. Далее, он назвал «главным сечением» нормальное сечение, перпендикулярное к плоскости хОу. Для этого и еще для другого нормального сечения, перпендикулярного к первому, получались уже более простые выражения радиуса кривизны. Обозначив затем через φ угол, образуемый плоскостью произвольного нормального сечения с плоскостью главного сечения, Эйлер снова составил общее выражение радиуса кривизны. Получившуюся опять-таки очень громоздкую формулу он несколько упростил и в качестве примеров взял цилиндр

z = √(aa — yy),

конус

z= √ (ппхх —уу)

и эллипсоид

zz = aa — тхх — пуу.

Только в конце работы он привел формулу радиуса кривизны в виде

,

из рассмотрения которой извлек важные заключения. Так, например, он нашел, что три известных радиуса кривизны позволяют определить все остальные его значения в точке поверхности, что в каждой точке поверхности существует наибольший радиус кривизны f и наименьший g, плоскости которых взаимно перпендикулярны и которые в свою очередь определяют общую кривизну элемента поверхности, а именно:

.

В статье, носившей то же название, что и работа Эйлера, Ж. Менье поставил целью развить результаты последней (Mem. div. sav., 1785; поступила в 1776). Но Менье исходил из совершенно иной концепции. Отправляясь от мысли, что совпадение частных дифференциалов до второго порядка включительно обусловливает совпадение кривизн двух поверхностей, Менье заменил в точке u, v, t (причем ось t лежала на нормали к поверхности в этой точке) поверхность параболоидом

.

Менье преобразовал это уравнение к виду

и затем доказал, что каждый элемент поверхности (термин Менье) можно получить вращением малой дуги окружности вокруг оси, параллельной касательной плоскости этого элемента. Для радиуса этой окружности r и расстояния оси от точки поверхности ρ он получил выражения

и

.

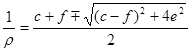переходящие одно в другое; при этом оказалось, что r и ρ совпадают с найденными Эйлером крайними значениями f и g радиусов кривизны нормальных сечений поверхности. К этому Менье присоединил теорему, носящую его имя. Именно, если R' есть радиус кривизны нормального сечения, проходящего через касательную AQ к кривой на поверхности, то R, радиус кривизны сечения, лежащего в другой плоскости, проходящей через AQ, определяется формулой R = R' sin ω, где ω — угол между обеими плоскостями. Отправляясь от этого, Менье дал полный разбор соотношений между кривизнами на элементе поверхности. Среди примеров он рассмотрел, в частности, задачу об определении поверхностей, для которых r=ρ. Интегрируя соответствующее дифференциальное уравнение, он получил, что

1=(Ax+B)2+(Ay+C)2+(Az+D)2

т. е., как и должно быть, уравнение шаровой поверхности. Вслед за тем он приступил к решению задачи об отыскании среди всех поверхностей, проходящих через контур, ограниченный данной пространственной кривой, поверхности с наименьшей площадью. С помощью своего способа образования элемента поверхности он вывел важное условие, r+r=0, а отсюда получил дифференциальное уравнение в частных производных минимальных поверхностей, найденное уже раньше другим способом Лагранжем [Misc. Taur., 1760/61 (1762)]. Частные интегралы этого уравнения дали ему в качестве примера минимальных поверхностей винтовую поверхность и катеноид. Принимая либо r, либо r равным бесконечности, Менье далее вывел дифференциальное уравнение развертывающихся поверхностей, данное уже Монжем, а в заключение доказал, что оба радиуса кривизны общих линейчатых поверхностей всегда бывают различного знака.

Политика Александра на завоёванных территориях. Её эволюция.
В этой главе мы рассмотрим лишь один (наиболее важный, как нам представляется) аспект политики Александра на завоёванных территориях. Это меры, предпринимаемые для создание социальной опоры власти македонского царя. Мы не рассматриваем здесь религиозную политику Александра, хотя она и имела важное значение в деле укрепления власти макед ...

Письмо как средство письменной коммуникации
В современном мире с его бурно развивающимися новыми электронными средствами коммуникации (факс, e-mail, Интернет) письмо, отправленное по почте или с курьером, при всей своей традиционности не утратило определенной значимости. Прежде всего, письмо, приходящее в запечатанном конверте, предназначено персонально лицу, указанному в качеств ...

Вторая пятилетка
В начале 1934 г. был утвержден план второй пятилетки (1933— 1937 гг.). Если за годы первой пятилетки, как считалось тогда, был построен экономический фундамент социализма, то главной задачей второго пятилетнего плана было построение социалистического общества. Среднегодовой прирост промышленной продукции должен был составлять 16,5%, Пре ...