Понятно, что столь ярко выраженный аналитический гений, каким являлся Эйлер, раз занявшись вычислительной тригонометрией, должен был значительно продвинуть ее вперед. Повод обратиться к тригонометрии представился ему в уже неоднократно упоминавшемся «Введении в анализ» (1748). В восьмой главе его первого тома Эйлер впервые ввел в анализ угловые функции как числовые величины, с которыми можно производить вычисления, как со всякими другими, так, чтобы впредь они уже не оказывали влияния на размерность выражений. И хотя Эйлер и не определил нигде тригонометрические функции явно как отношения сторон прямоугольного треугольника, но всегда рассматривал их именно так. Если отвлечься от несущественных мелочей, то изложение и символика Эйлера были вполне современными. Уже в одной работе в Coram. Ac. Petr., 1729 (1735) он записал теорему косинусов сферической тригонометрии в виде

cos : ВС = cos : АВ • cos : AC + cos A • sAB • sAC;

целый синус, который все еще употребляло большинство прежних авторов, здесь уже был принят равным 1. Обозначения тригонометрических функций во «Введении» были таковы: sin. A. z или sin. z (A = arcus), cos. A. z или cos. z, tang. z, cot. z и т. д.

В начале названной главы были впервые систематически установлены формулы для sin (z + ), sin (z+p) и т. д. Написав:

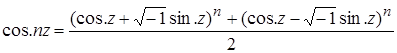
Эйлер раскрыл скобки и получил таким путем формулу для cosnz; аналогично он нашел формулу для sinnz. Беря п бесконечно большим, a z бесконечно малым, так что cosz=l и sinz=z, он вывел из этих формул бесконечные ряды для синуса и косинуса. Отсюда он получил ряды для синуса, косинуса, тангенса и котангенса , отчасти опубликованные им уже в Comm. Ac. Petr., 1739 (1750). Затем он исчерпывающим образом показал, как можно использовать эти ряды для вычисления тригонометрических таблиц. Позднее в Nov. Comm. Ac. Petr., 1754/55 (1760) он вывел дальнейшие ряды для sinnj, cosnj, sinmj, cosnj, следующие по функциям углов, кратных j. На связь между показательной и тригонометрическими функциями Эйлер натолкнулся уже в одной работе о рядах, помещенной в Comm. Ac. Petr., 1740 (1750). Соответствующую определяющую формулу для синуса он дал в Misc. Berol., 1743, но доказаны были формулы для синуса и косинуса только во «Введении». О результатах Эйлер, очевидно, ничего не знал. Формулы

cos х = (eix + e-ix) и sin x = (eix — e-ix)

он получил во «Введении» из выражений

и

полагая п = ¥. К этому он присоединил еще формулу

Определение sin(x+iy) и cos(x+iy) он впервые дал в Mem. Ac. Berl., 1749.

Суммирование рядов синусов и косинусов, аргументы которых растут в арифметической прогрессии, Эйлер произвел уже в Misc. Berol., 1748. Во «Введении» он вновь вернулся к этому вопросу с более общей точки зрения. Позднее (Opuscul. anal., Петербург, 1783) он занялся аналогичными рядами, аргументы которых образуют геометрическую прогрессию. Представлением тригонометрических функций в виде произведений Эйлер начал заниматься уже в Comm. Ac. Petr., 1734/35 (1740), где разложил в бесконечное произведение синус. То же самое он провел для синуса и косинуса в Comm. Ac. Petr., 1740 (1750) и Misc. Berol., 1743. Все это вместе с некоторыми дополнениями было включено во «Введение», в 14-й главе которого он также детально занялся вопросом об умножении и делении углов, т. е. о тригонометрических функциях кратных углов. Мы указывали в первой части, что в этих разнообразных исследованиях Эйлер действовал более творчески, нежели критически. Это столь глубоко коренилось в его натуре, что он оставил без внимания возражения, сделанные ему главным образом Николаем I Бернулли уже в 1742 и 1743. Эйлер продолжал производить вычисления над любыми бесконечными рядами, распространял теоремы о конечных многочленах на бесконечные и придавал любые значения индексу п, в начале доказательства считавшемуся целочисленным. Несмотря на это, получаемые им результаты обычно бывали справедливы, хотя в некоторых случаях он пришел и к ошибочным выводам, как, например, в упоминавшейся статье в Nov. Comm. Ac. Petr., 1754/55 (1760).

Зарождение классового общества. Рабовладельческие государства в Северном Причерноморье и Крыму. Государственные объединения племен киммерийцев и тавров
В начале I тысячелетия до н.э. население Восточной Европы вступило в новую историческую эпоху - железный век. Научившись добывать железо, изготовлять и применять железные" орудия труда, более крепкие, чем медные и бронзовые, первобытные люди достигли значительного повышения производительности своего труда. У старейшин родов и вожде ...

Гонконг
Гонконг - крупнейший порт, промышленный, финансовый и внешнеторговый центр, город-звезда в Азиатско-тихоокеанском регионе. В этом динамичном, процветающем, жизнерадостном, многогранном, многонациональном городе, голоса 6,6 миллионного населения утопают в каскаде золотых высотных зданий. С 1 июля 1997 года - Особый Административный Район ...

Неразгаданные тайны битвы
а) Где же находится место сражения? До сих пор точно неизвестно даже место битвы. Его отечественные историки ищут с середины XIX века. Причем одни считают, что Ледовое побоище развернулось на западном берегу Чудского озера, другие – на западном берегу Псковского. А некоторые исследователи указывают на Теплое озеро. Если предположить, ч ...